一、概念

Definition
1. 概念：反映思维对象特有属性（或本质属性）的思维形态。
2. 语词
3. 对象
4. 属性
  1. 特有属性
  2. 偶有属性
5. 概念的逻辑特征
  1. 内涵
  2. 外延
概念与语词的联系和区别：
1. 联系：语词是概念的语言形式；概念是语词的思想内容。
2. 区别：
  1. 概念必须通过语词表达，但并非所有语词都表达概念；
  2. 概念和语词不是一一对应的。即不同的语词在不同语境中可以表达同一个概念（语词不同，语义相同）
概念的种类
1. 按概念外延的数量分
  1. 普遍概念：反映一类对象的概念，外延至少有两个对象。
  2. 单独概念：反映某个特定对象的概念，外延只有一个对象。
    
    用于表达的语词形式：
    1. 专名（专有名称）：北京、亚里士多德
    2. 摹状词（描述特定对象的短语）：中国的首都、《工具论》的作者
  3. 空概念：反映空类的概念。如“独角兽”。
    
    此处的空概念定义为现实世界中不存在的概念，可能在想象世界/可能世界中存在。
2. 按概念的外延所反映的对象是否为集合体来分类
  1. 集合体：由若干对象组成的整体，其中每一个对象称为这个集合体的“个体”。
    
    个体组成集合体，但不具有集合体的属性，即整体与部分的关系。
  2. 非集合体：由若干对象组成。对象组成非集合体，必然具有非集合体的属性，即一般与个别的关系。
  3. 集合概念 / 非集合概念：森林 / 树
3. 按概念的内涵所反映的对象是否具有某种属性来分类
  1. 正概念（肯定概念）：反映事物具有某种属性的概念
  2. 负概念（否定概念）：反映事物不具有某种属性的概念
  3. 正负概念总是成对出现
  4. 正负概念在形式结构上有如下关系：
    
    $$ 负概念=(否定词+正概念) $$
概念的集合使用和非集合使用
1. Definition：在不同语境中，同一语词既可以表达集合概念，也可以表达非集合概念，这就是概念的集合使用与非集合使用。
2. 判断上来看，如果在概念前面加一个量词说得通，就是非集合概念。
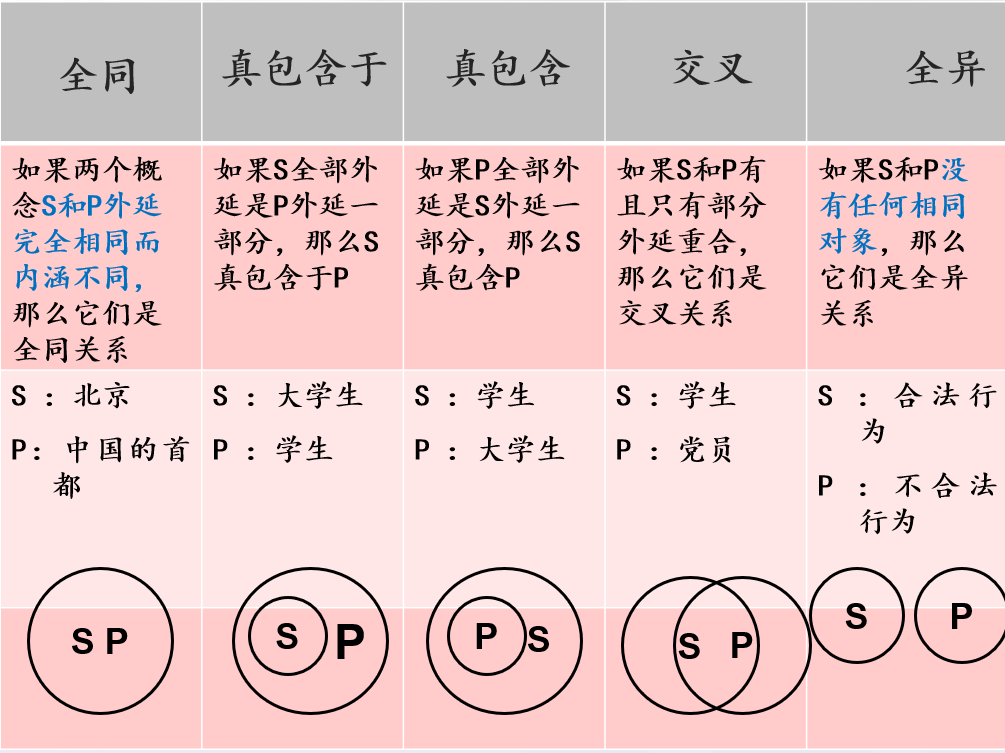
概念之间外延关系（不会的请重修高中政治选必四）
1. 全同关系、真包含于关系、真包含、交叉、全异关系。
2. 在传统逻辑中，将“真包含于”关系和“真包含”关系统称为**“属种关系”**。请注意，是在传统逻辑中！
  
  不会的请重修高中政治选必四。
3. 全异关系又分为矛盾关系和反对关系。
  
  矛盾关系：$S+P=U$.
  
  反对关系：$S+P<U$.
内涵与外延的反变关系
1. 具有属种关系的概念的内涵与外延之间存在反变关系。
2. 反变关系：一个概念的内涵越少，则其概念的外延越大；反之，一个概念的内涵越多，其外延越小。
3. 属种概念之间内涵与外延反变关系，是对概念进行限制和概括的逻辑根据。
概念的限制、概括及应注意的问题

二、定义

定义
1. Definition：用简明的形式揭示概念内涵的逻辑方法。
2. 组成：被定义项、定义项、定义联项
  
  （定义联项：表示被定义项与定义项的逻辑关系并联结它们的概念）
3. 一般形式：$D_s$就是$D_p$。其中，$D_s$是被定义项，$D_p$是定义项。
4. 内涵：思维对象的特有属性；
  
  外延：具有此属性的一类对象。
5. 定义用于明确概念的内涵，划分用于明确概念的外延。
6. 类、子类 = 属、种
现代定义的三大类型
1. 内涵定义：种差法（属+种差）
  
  $$ 被定义项=种差+邻近的属 $$
  - 种差：在同一个属概念下，同层次的种概念之间的差别，并且这种差别为被定义项所共有。
  内涵定义的不同种类：性质定义、发生定义、功用定义、关系定义
  
  范畴作为一定论域中最大的属，不适用种差法。
  
  单独概念指称单独对象，不适合用种差法。
2. 语词定义：界定语词标准用法或特殊用法
  1. 分为报道性定义（词典定义）、约定性定义、修正性定义（精确定义）
3. 外延定义：列举一概念的外延
  1. 分为穷举定义、例举定义、实指定义
  - eg. “近亲属”指夫、妻、父、母、子、女、同胞兄弟姐妹。
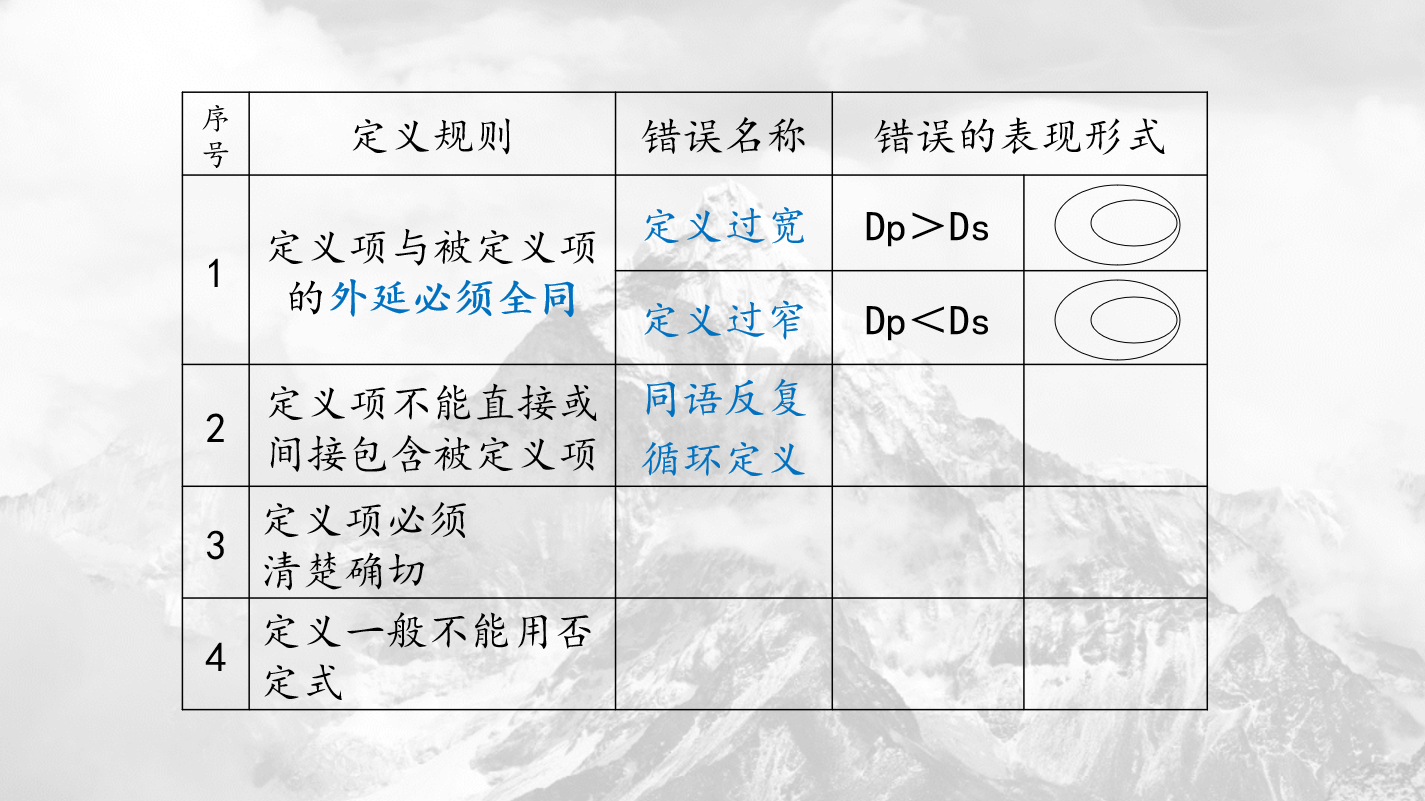
定义的规则
1. 定义项与被定义项的外延必须全同。
  
  违反则犯“定义过宽/定义过窄”的错误。
  
  太阳是白昼发光的星体。
2. 定义项不能直接或间接包含被定义项。
  
  违反则犯”同语反复（循环定义）“的错误。
3. 定义项必须清楚确切。不可使用比喻的手法。
  
  违反则犯”含混不清“的错误。
4. 定义一般不使用否定式
  1. 特殊情况：当种差为负概念，或定义联项为否定形式，那么可以使用否定定义。

三、划分

Definition: 揭示概念外延的逻辑方法
组成：母项、子项、划分标准。母项和子项是属种关系。
整体与部分不是属种关系。要将“划分”与“分解”区别开来。

当你不能说A是B的一种时，它就不属于属种关系。
方法：一次划分、连续划分、二分法。

二分法中，两子项具有矛盾关系，正概念与负概念
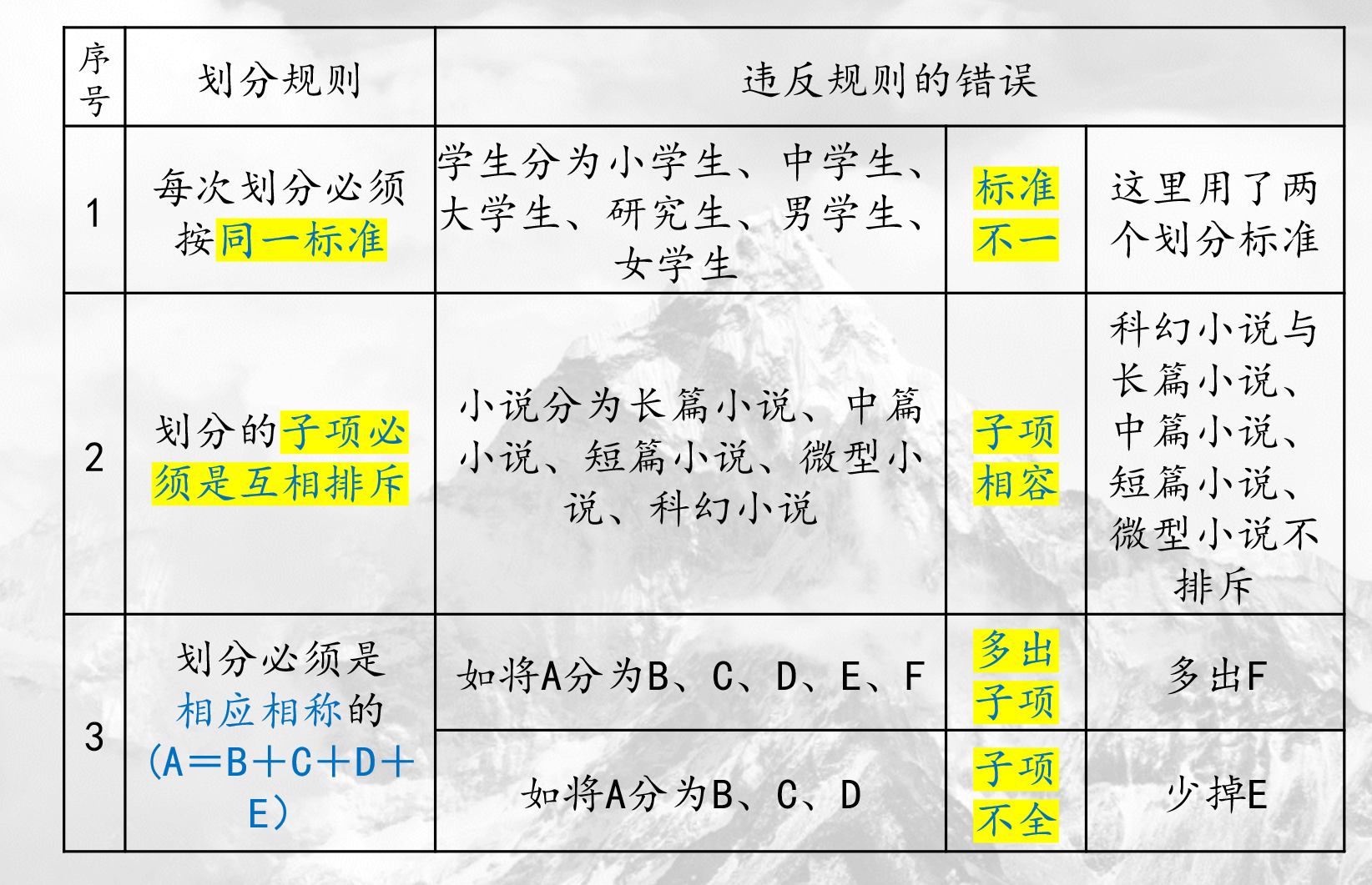
规则：
1. 每次划分必须按照同一个标准。否则犯“标准不一”的的错误。
2. 子项必须互相排斥，应为全异关系，不能是属种关系、交叉关系。否则犯”子项相容”的错误。
3. 划分后，各子项外延之和必须等于母项外延。否则犯“子项不全”、“多出子项”的错误。

四、论证

包括证明和反驳。（即立论、驳论）。
1. 证明是用一个或一些已知为真的命题去确定另一命题为真或成立的思维过程。
2. 反驳是用一个或一些已知为真的命题去确定另一命题为假或不成立的思维过程。
组成：
1. 论题：论证中需要证明或反驳的命题。解决“论证什么”的问题。
2. 论据：论证中用以确定论题真实性或虚假性的命题。解决“用什么论证”的问题。
3. 论证方式：论证中使用的推理形式。解决“如何论证”的问题。
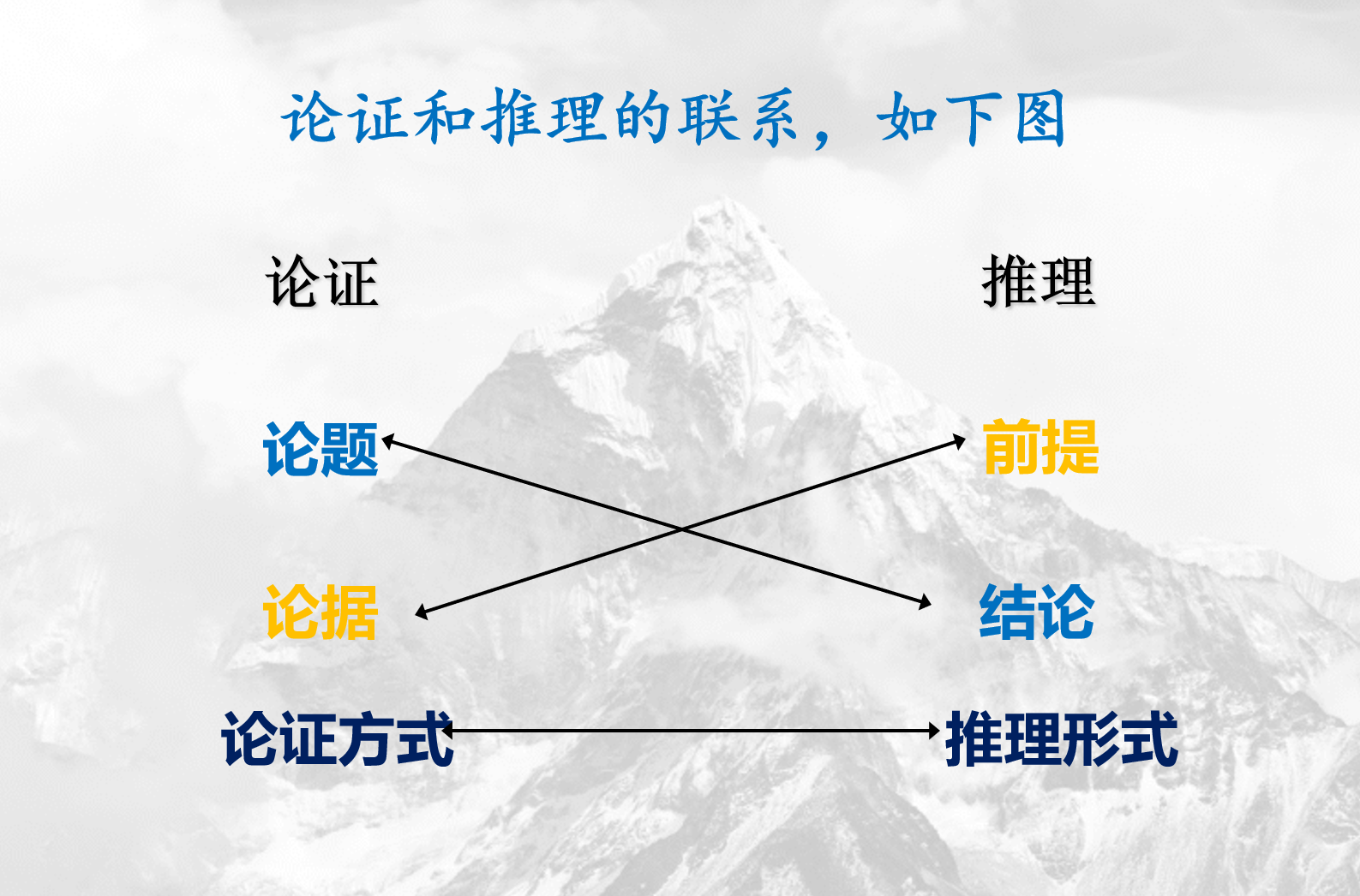
论证和推理的联系
论证和推理的区别
1. 思维进程不同。从论题到论据 / 从前提到结论
2. 逻辑要求不同。论证要求证据内容为真且形式正确，推理只要求形式正确。
3. 论证一般比推理复杂，是推理的综合运用。
充足理由原则
1. 定义：在思维和论证过程中，任何正确的思想，必然有其充足理由。
  
  A真，是因为B真且B足以推出A。则此时，B是A的充足理由。
2. 逻辑要求：理由必须真实且充分（推理前提真实、推理形式有效）。

五、证明

按推理形式不同，分为演绎证明、归纳证明和类比证明；

按是否与论题直接发生联系，分为：

直接证明：根据论据的真实性，通过逻辑推理直接确定论题真实性的论证。

间接证明：用论据确定与论题相矛盾或具有下反对关系的反论题的虚假，根据排中律确定论题真实性。（反证法、选言证法）

区分直接和间接，主要看论证是否直接从原论题出发。
1. 反证法：设立反论题，通过确定反论题为假，根据排中律确定原论题为真。
  
  在逻辑推理中，前真不能推出后假。蕴含关系只在此情况中不成立。所以当后件为假时，前件一定为假。故在此关系中，逻辑是通顺的。方式为充分条件假言推理否定后件式。
  
  $$ 假设\lnot p\Rightarrow q，\\由于\lnot q=True, \\所以\lnot(\lnot p)\Rightarrow p=True $$
2. 选言证法：通过确定除论题之外其余可能情况都为虚假，从而推出论题为真的一种间接证明方法。又叫排除法、淘汰法
  
  本质上是将非p的所有情况拆解成了q和r两方面。遵循排中律进行证明。
  
  方式为相容选言推理的否定肯定式。
  
  $$ p\lor(q+r)成立，必有一真\\由于q+r=False,则p=True $$

六、反驳

反驳是对某一具体证明过程或立论的论题的证伪。
包括：反驳论题、反驳论据、反驳论证方式。
反驳论题和论据的方式：
1. 直接反驳：
  1. 用论据直接确定被反驳论题的虚假。
  2. 归谬反驳：从被反驳论题引出互相矛盾的命题，进而证明被反驳论题是假的。
    
    依然是一个充分条件假言推理否定后件式。归谬法。
    
    $$ p\Rightarrow q, 由于\lnot q=True, 所以\lnot p =True $$
2. 间接反驳
  1. 设立与被反驳论题具有矛盾关系或反对关系的反论题，通过证明反论题的真实，并根据矛盾律的要求，从而确定被反驳论题的虚假性。
  2. 步骤：设立反论题；独立证明反论题为真；根据矛盾律，由反论题真，确定原论题假。（由真推假）
间接证明和间接反驳的不同点
1. 目的不同：一个是论证，一个是反驳
2. 基本规律不同：间接证明根据排中律，简介反驳根据矛盾律。
3. 论题与反论题关系不同：证明中二者具有矛盾关系或下反对关系，反驳中具有矛盾关系或反对关系
反驳论证方式
1. 指出对方在论证中违反逻辑规律要求或推理规则，即论据“推不出”论题。
2. 也可以使用归谬法。先假定其论证方式正确，再按同样的论证方式推导出荒谬的结论，从而否定其论证方式。
3. 论证方式无效不等于论题、论据无效，只可以说明论题的真实性可疑。sus。

七、论证规则

关于论题：
1. 论题必须清楚、明确——“论旨不清”
2. 论题必须始终同一——“转移/偷换论题、论证过少/过多”
关于论据：
1. 必须是已知为真的命题——“虚假理由/预期理由”
2. 真实性不能依赖论题来证明——“循环论证”
关于论证方式：
1. 从论据应能推出论题——“推不出”
2. 推不出有以下情况：
  1. 违反推理规则或违反逻辑规律要求
  2. 论据、论题无关
  3. 论据论题必要但不充分——“理由不充足”